
🔎 주제
이번 포스팅에서는 자료구조와 알고리즘에서 알고리즘의 성능을 따질 때 중요한 표기법인 Big O 표기법의 개념을 살펴보고, 몇 가지 예시를 들어보고자 한다.
Big O 표기법
알고리즘의 복잡도를 나타낼 때 Big Θ, Big Ω 표기법 등 여러 방법이 있지만
가장 많이 쓰는 건 Big O 표기법인 듯 하다.
정의
알고리짐의 성능을 나타내는 법으로 알고리즘이 얼마나 빠르고 효율적인지를 수로 표현한다.
알고리즘에서 효율을 계산할 때 중요한 건 '데이터의 수가 많아질 때 연산 횟수는 얼마나 증가하는가?'이고 Big O는 알고리즘이 성능이 최악인 경우를 나타날 때 사용한다.
따라서 해당 알고리즘을 사용하는 어떤 경우에도 보장되는 성능 표기법이다.
알고리즘의 성능?
알고리즘의 성능은 1. 코드의 실행 속도(시간)과 2. 코드 실행 시 필요한 메모리의 양으로 평가된다.
Big O 표기법으로는 시간 복잡도와 공간 복잡도를 분석할 수 있다.
- 시간 복잡도: 코드가 실행되는데 걸리는 시간
- 입력 데이터 개수(n)가 늘어날수록 컴퓨터가 그 작업을 처리하는데는 얼마나 실행 시간이 늘어날까?
- 공간 복잡도: 코드가 실행되면서 사용되는 메모리 양
- 입력 데이터 개수(n)가 늘어날수록 얼마나 많은 양의 데이터가 메모리에 저장되어야 할까?
수학적 정의
수학적으로 나타낸 정의는 다음과 같다. 개인적으로 이 정의가 맘에 든다.
f(n) = O(g(n)) iff there exist positive costants c and n0 such that f(n)≤ c·g(n) for all n, n≥n₀
모든 n, n≥n₀ 에 대하여 f(n)≤ c·g(n) 를 만족하는 양의 상수 c 와 n0 가 존재하면 f(n) = O(g(n)) 이다.
이때 f(n) 은 _g(n)_의 Big O라고 읽는다.
예를 들어 _f(n)_과 _g(n)_이 다음과 같다고 하자. 평가하려는 (시간복잡도 or 공간복잡도) 함수가 _f(n)_이고, _g(n)_은 비교할 함수이다.
f(n) = 3n+2
g(n) = n
이때 3n₀+2≤ cn₀을 만족하는 c=4, n₀=2이다. 조건을 만족하는 c와 n₀이 있으므로 f(n) = 3n=2 = _O(n)_이다.
여기서 두드러지는 Big O 표기법의 특징은
- 상수항을 무시한다.
_O(2n)_이든 _O(3n+1)_이든 _O(n)_이다. - 최고차항만 본다.
데이터 입력 개수 n의 영향을 받으므로 가장 영향력이 큰 최고차항만 본다.
_O(3n²+2n+1)_은 _O(3n²)_으로, 여기서 _O(n²)_으로 보면 된다.
아래 그래프는 Big O 표기법에서 주로 사용되는 표기들의 입력 개수에 따른 성능 차이를 나타낸 것이다.
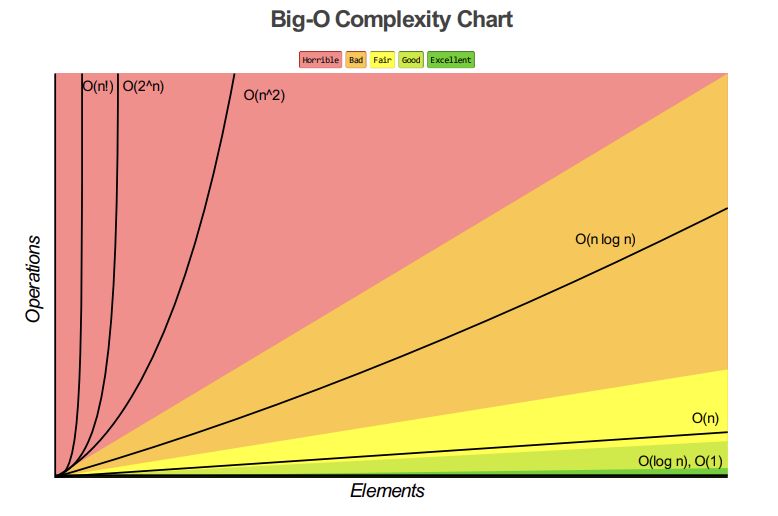
Big O에서 시간 복잡도를 따지면 다음과 같다. g(n)이 상수에 가까울수록 효율이 좋다.
O(1) < O(log n) < O(n) < O(nlogn) < O(n²) < ...
시간 복잡도 🔽 ---------------시간 복잡도 ⏫알고리즘 성능이 빨간색으로 넘어간다면 수정이 필요할 것이다.
예시와 실습
알고리즘 강의에서 주로 정렬과 탐색 알고리즘을 예시로 배워
그와 관련된 실생활 사례를 가지고 왔다.
O(n)
O(n)=f(n)=n으로 O(n)은 하나씩 확인하는 선형 알고리즘에 해당한다.
최악의 경우 입력 데이터 n개를 모두 확인한다.
실생활 예시

도서관에서 공부에 필요한 책을 빌리려고 하는데, 도서관의 책들이 아직 정리되지 않은 상태이다.
한 권씩 꺼내 제목을 확인하며 책을 찾는다.
운이 없다면, 도서관의 모든 책 n개를 확인해야 한다.
이런 식의 탐색을 선형 탐색이라고 한다.
코드
public class LinearSearch {
public static int linearSearch(String[] arr, String target) {
for (int i = 0; i < arr.length; i++) {
if (arr[i].equals(target)) return i; // 찾으면 인덱스 반환
}
return -1; // 찾지 못한 경우
}
public static void main(String[] args) {
String[] arr = {"코딩의 이해", "개발자가 되고 싶어?", "스프린트",
"알고리즘 파헤치기","자료구조의 정석"};
System.out.println(linearSearch(arr, "스프린트")); // 2
}
}
O(log n)
실생활 예시

사전에서 어떤 단어를 찾으려고 한다.
사전은 당연히 ㄱㄴㄷ, 혹은 ABC 순서로 정렬된 상태라고 가정한다.
처음부터 찾는 게 아니라 중반부터 찾아가며 확인해야 하는 페이지를 절반씩 줄인다.
얘를 들어 "Notation" 뜻이 궁금하다면,
일단 사전에서 중간 페이지의 단어와 Notation의 알파벳을 비교한다.
n이 뒷쪽에 있다면 이제 중간 페이지의 뒷부분들만 확인하면 된다.
이런 식으로 절반씩 줄여나간다. 이러한 탐색을 이진 탐색이라고 한다.
코드
import java.util.Arrays;
public class DictionarySearch {
public static int binarySearchDictionary(String[] dictionary, String target) {
int left = 0, right = dictionary.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
int comparison = dictionary[mid].compareTo(target);
if (comparison == 0) return mid; // 단어를 찾았을 경우 인덱스 반환
else if (comparison < 0) left = mid + 1; // target이 사전 순으로 뒤쪽이면 오른쪽 탐색
else right = mid - 1; // target이 사전 순으로 앞쪽이면 왼쪽 탐색
}
return -1; // 단어가 사전에 없는 경우
}
public static void main(String[] args) {
String[] dictionary = {"algorithm", "data", "character", "map", "notation", "object", "public", "static"};
Arrays.sort(dictionary); // 사전은 정렬되어 있어야 함
String target = "notation";
int result = binarySearchDictionary(dictionary, target);
if (result != -1) {
System.out.println("단어 '" + target + "'는 사전의 " + result + "번째 인덱스에 있습니다.");
} else {
System.out.println("단어 '" + target + "'를 찾을 수 없습니다.");
}
}
}+
왜 절반씩 줄여가는 것이 O(log n)일까?
1️⃣ 한 단계 진행할 때마다 검색할 페이지 수가 절반으로 줄어든다.
사전의 총 페이지 수를 n이라고 하면,
- 첫 번째 비교 후 n/2 개의 페이지만 확인하면 됨
- 두 번째 비교 후 n/4 개의 페이지만 확인하면 됨
- 세 번째 비교 후 n/8 개의 페이지만 확인하면 됨
- k번째 비교 후 n / 2ᵏ 개의 페이지만 확인하면 됨
2️⃣ 언제 검색이 끝나는지 계산
이진 탐색은 보통 1개의 페이지만 남았을 때 종료한다.
n / 2ᵏ = 1이 되는 k를 구하기 위해 양변에 log를 적용하면
log₂n= k
즉, 이진 탐색의 최대 비교 횟수 k는 log₂(n) 이고
Big O 표기법에 따라 O(log n)이다.
O(n∙log n)
- 병합 정렬, 퀵 정렬, 힙 정렬 등이 속한다.
그 중 병합 정렬은 배열을 계속 반으로 나눈 후, 정렬된 상태로 다시 합치는 '분할 정복' 알고리즘을 사용한다.
실생활 예시
대학 입시에서 수 천에서 수 만의 지원자의 성적을 정렬해야 하는 경우
어떻게 정렬할 것인가?
코드
import java.util.Arrays;
public class MergeSort {
public static void mergeSort(int[] arr) {
if (arr.length < 2) return; // 배열이 하나 이하의 원소만 있으면 정렬할 필요 없음
int mid = arr.length / 2; // 중간 지점
int[] left = Arrays.copyOfRange(arr, 0, mid); // 왼쪽 부분 배열
int[] right = Arrays.copyOfRange(arr, mid, arr.length); // 오른쪽 부분 배열
mergeSort(left); // 왼쪽 배열 정렬
mergeSort(right); // 오른쪽 배열 정렬
merge(arr, left, right); // 정렬된 배열을 합치기
}
private static void merge(int[] arr, int[] left, int[] right) {
int i = 0, j = 0, k = 0;
while (i < left.length && j < right.length) {
if (left[i] <= right[j]) arr[k++] = left[i++]; // 작은 값을 배열에 넣기
else arr[k++] = right[j++];
}
while (i < left.length) arr[k++] = left[i++]; // 남은 요소 추가
while (j < right.length) arr[k++] = right[j++];
}
public static void main(String[] args) {
int[] arr = {10, 3, 8, 4, 7, 1, 2, 5, 9, 6};
mergeSort(arr);
System.out.println(Arrays.toString(arr)); // [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
}
}+
왜 병합 정렬은 O(n∙log n)일까?
앞서 말한 분할 정복 알고리즘과 관련 있다.

절반씩 나누는 분할은 이진 탐색에서 확인했듯이 O(log n)의 시간이 필요하고,
분할을 하나의 원소가 남을 때까지 반으로 나누므로, n개의 배열이 생기고 이 정렬된 배열을 n번 합쳐야 한다. 따라서 합병에서 O(n)이 소요된다.
이 둘을 곱해 병합 정렬에서는 O(n∙log n)의 시간 복잡도를 가진다.
📋 참고자료
Thomas H. Cormen et al. "Introduction to Algorithms (3rd Edition)" (MIT Press, 2009)
빅오 표기법 (big-O notation) 이란
[알고리즘] 시간 복잡도와 Big O 표기법
'⚙️ CS > 📚 자료구조 & 알고리즘' 카테고리의 다른 글
| [자료구조] 비선형 자료 구조 개념 정리 | 그래프, 트리, 힙, 우선순위 큐, 셋, 맵, 해시 테이블 (0) | 2025.10.18 |
|---|---|
| [자료구조] 선형 자료 구조 (0) | 2025.10.02 |
| [알고리즘] 시간 복잡도와 공간 복잡도 + Big O 표기법 (0) | 2025.10.02 |